Dando continuidade ao estudo, você entenderá o que é proporção e que um elemento pode ser proporcional ao outro.
Retomará o assunto sobre razão entre as grandezas, dessa vez, aplicada as proporções.
Como?
Ex.: Para fazer a receita de um bolo, é necessário que você aplique as proporções de produtos como: azeite,
farinha de trigo e ovos.
Se para fazer um bolo você precisa de 3 ovos, proporcionalmente, para fazer 3 bolos, precisará de 9 ovos, certo?
Então aprenderá um pouco mais!
Ao final do capítulo você terá subsídios para:
Termos são a relação entre os objetos de uma dimensão com outra. Desta forma, é possível comparar a base com a altura de dois objetos, e esta comparação é chamada de termos. A partir desta relação é possível obter uma razão, ou seja, a proporção das dimensões entre um objeto e outro. Observe:

A razão entre a altura e a base do primeiro retângulo é 6/4 = 1,5.
Já a razão entre a altura e a base do segundo retângulo é 3/2 = 1,5.
Então é possível afirmar que:
6/4 = 3/2
Essa igualdade é chamada de proporção.
Para 6/4 = 3/2, poderá ser representado como 6:4 = 3:2
A leitura destes termos ficaria da seguinte maneira:
“seis está para quatro, assim como três está para 2.”

Com o estudo que acabamos de realizar, vimos que é possível obter a razão dos termos por meio da proporção das dimensões entre dois objetos.


Duas grandezas são diretamente proporcionais, se os valores a e b correspondentes são tais que a/b = k , onde k é um valor constante, positivo, chamado de constante da proporcionalidade.
Duas grandezas são inversamente proporcionais, se os valores a e b correspondentes são tais que a.b=k, onde k é um valor constante, positivo, chamado de constante de proporcionalidade inverso.
Exemplo:
O voo do avião a jato
Um avião que voa a 500 km/h percorre a distancia entre duas cidades em 3 horas.
Quanto tempo gastará o avião para percorrer a mesma distancia se voar a 750km/h?


APLICAÇÃO
Dando segmento ao estudo de proporções, vocês verão três tipos de aplicação para situações distintas.
Para aplica-las, deverão analisar os termos da equação, verificar se são proporcionais ou inversamente
proporcionais e calcular sua razão.
Veja a seguir:
Aplicação 1
Vimos anteriormente que, em uma viagem, quanto maior a velocidade média, menor será o tempo gasto. Nesse caso,
quanto menor for a velocidade, maior será o tempo. Observe a tabela.
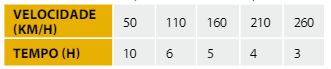
Como podem perceber, essas grandezas são inversamente proporcionais, ou seja, se viajo mais rápido, levo menos tempo ou se viajo mais devagar, levo mais tempo.
Aplicação 2
Para entender esta segunda forma de aplicação, imagine que você tenha comprado um copo de refrigerante, que
corresponde a 250ml. Se um professor comprou refrigerante suficiente para encher 39 copos, quantos litros da
bebida o professor comprou?
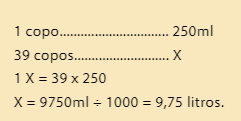
Aplicação 3
Suponha que uma roda d’água realiza 45 rotações por minuto. Quantas voltas essa roda daria em 4 segundos?


